Understanding Self-Attention in Transformers: A Visual Breakdown

🔍 Understanding Self-Attention in Transformers: A Visual Breakdown #

This document summarizes key questions about self-attention, embedding vectors, positions, and the input matrix in Transformers — using the image you provided as the foundation.

🧠 What Is Happening in the Diagram? #

The figure shows how self-attention computes the output for a specific position (“detection”) by:

  • Generating attention weights between that position and all other positions.
  • Using those weights to compute a weighted sum of the input feature vectors.

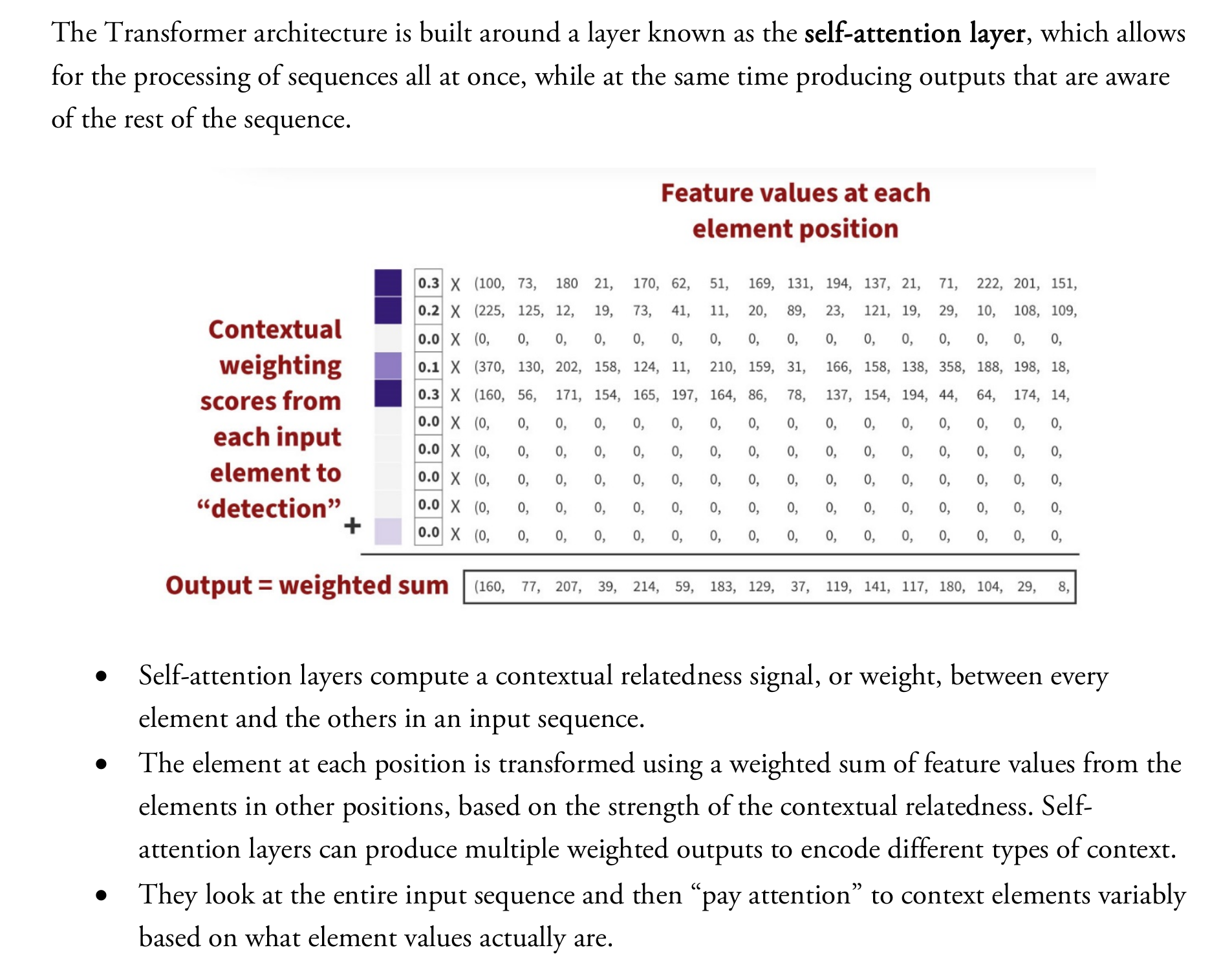
Self-Attention Diagram

🧩 Key Concepts Explained #

Term Meaning
Element A token or word in the input sequence. Each row in the matrix is one.
Position The index (0-based) of each element. Used to maintain order.
Sequence The full ordered list of elements (e.g. a sentence).
Word The natural-language item each element may represent.
Feature Values Vector representation of the element (its embedding).
  • While element and position are tightly linked (1:1), they are conceptually distinct:
    • Position = slot/index
    • Element = content in that slot

🧮 How Attention Scores Are Computed #

Self-attention uses scaled dot-product attention:

  1. Input matrix X (from the figure) holds all embeddings.
  2. It is projected into Q, K, V using learned weights.
  3. Attention scores = dot(Q[i], K[j]) / sqrt(d_k)
  4. Softmax turns scores into attention weights.
  5. Output vector = weighted sum over all V[j], using those weights.

The purple bar on the left in the figure shows these attention weights (e.g., [0.3, 0.2, 0.1, 0.3, 0, ...]).

✅ What the Image Represents #

Part of Image Concept in Transformer
Right-side matrix (rows) Input feature matrix X
Each row One input element (word/token)
Left-side purple weights Attention scores for one position
Final row at bottom Output vector (weighted sum of inputs)

Prepared with explanations from ChatGPT based on your questions.